Chapter 15 Stream Connectors
The two basic variable types in a connector – “potential” (or across) variable and “flow” (or through) variable – are not sufficient to describe in a numerically sound way the bi-directional flow of matter with convective transport of specific quantities, such as specific enthalpy and chemical composition. The values of these specific quantities are determined from the upstream side of the flow, i.e., they depend on the flow direction. When using across and through variables, the corresponding models would include nonlinear systems of equations with Boolean unknowns for the flow directions and singularities around zero flow. Such equation systems cannot be solved reliably in general. The model formulations can be simplified when formulating two different balance equations for the two possible flow directions. This is not possible with across and through variables though.
This fundamental problem is addressed in Modelica by introducing a third type of connector variable, called stream variable, declared with the prefix stream. A stream variable describes a quantity that is carried by a flow variable, i.e., a purely convective transport phenomenon. The value of the stream variable is the specific property inside the component close to the boundary, assuming that matter flows out of the component into the connection point. In other words, it is the value the carried quantity would have if the fluid was flowing out of the connector, irrespective of the actual flow direction.
The rationale of the definition and typical use cases are described in Appendix D.
15.1 Definition of Stream Connectors
If at least one variable in a connector has the stream prefix, the connector is called “stream connector” and the corresponding variable is called “stream variable”. The following definitions hold:
-
•
The stream prefix can only be used in a connector declaration.
-
•
A stream connector must have exactly one scalar variable with the flow prefix. [The idea is that all stream variables of a connector are associated with this flow variable].
-
•
For every outside connector [see section 9.1.2], one equation is generated for every variable with the stream prefix [to describe the propagation of the stream variable along a model hierarchy]. For the exact definition, see the end of section 15.2.
-
•
For inside connectors [see section 9.1.2], variables with the stream prefix do not lead to connection equations.
-
•
Connection equations with stream variables are generated in a model when using the inStream() operator or the actualStream() operator, see section 15.2 and section 15.3.
[Example:
FluidPort is a stream connector, because some connector variables have the stream prefix. The Medium definition and the stream variables are associated with the only flow variable (m_flow) that defines a fluid stream. The Medium and the stream variables are transported with this flow variable. The stream variables h_outflow and X_outflow are the stream properties inside the component close to the boundary, when fluid flows out of the component into the connection point. The stream properties for the other flow direction can be inquired with the built-in operator inStream(). The value of the stream variable corresponding to the actual flow direction can be inquired through the built-in operator actualStream(), see section 15.3.]
15.2 Stream Operator inStream and Connection Equations
In combination with the stream variables of a connector, the inStream() operator is designed to describe in a numerically reliable way the bi-directional transport of specific quantities carried by a flow of matter.
inStream(v) is only allowed on stream variables v and is informally the value the stream variable has, assuming that the flow is from the connection point into the component. This value is computed from the stream connection equations of the flow variables and of the stream variables.
For the following definition it is assumed that N inside connectors mj.c (j=1,2,…,N) and M outside connectors ck (k=1,2,…,M) belonging to the same connection set [see definition in section 9.1.2] are connected together and a stream variable h_outflow is associated with a flow variable m_flow in connector c.
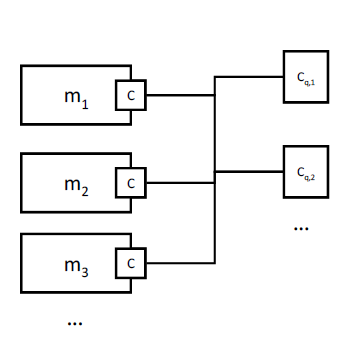
[The connection set represents an infinitesimally small control volume, for which the stream connection equations are equivalent to the conservation equations for mass and energy.]
With these prerequisites, the semantics of the expression inStream(mi.c.h_outflow) is given implicitly by defining an additional variable h_mix_ini, and by adding to the model the conservation equations for mass and energy corresponding to the infinitesimally small volume spanning the connection set. The connection equation for the flow variables has already been added to the system according to the connection semantics of flow variables defined in section 9.2.
Whenever the inStream() operator is applied to a stream variable of an inside connector, the balance equation of the transported property must be added under the assumption of flow going into the connector
Note that the result of the inStream(mi.c.h_outflow) operator is different for each port i, because the assumption of flow entering the port is different for each of them.
Additional equations need to be generated for the stream variables of outside connectors.
Neglecting zero flow conditions, the solution of the above-defined stream connection equations for inStream values of inside connectors and outflow stream variables of outside connectors is (for a derivation, see Appendix D):
Note, that inStream(ck.h_outflow) is computed from the connection set that is present one hierarchical level above. At this higher level ck.h_outflow is no longer an outside connector, but an inside connector and then the formula from above for inside connectors can be used to compute it.
If the argument of inStream() is an array, the implicit equation system holds elementwise, i.e., inStream() is vectorizable.
The stream connection equations have singularities and/or multiple solutions if one or more of the flow variables become zero. When all the flows are zero, a singularity is always present, so it is necessary to approximate the solution in an open neighbourhood of that point. [For example assume that mj.c.m_flow = ck.m_flow = 0, then all equations above are identically fulfilled and inStream(..) can have any value]. However, specific optimizations may be applied to avoid the regularization if the flow through one port is zero or non-negative, see Appendix D. It is required that the inStream() operator is appropriately approximated when regularization is needed and the approximation must fulfill the following requirements:
-
1.
inStream(mi.c.h_outflow) and inStream(ck.h_outflow) must be unique with respect to all values of the flow and stream variables in the connection set, and must have a continuous dependency on them.
-
2.
Every solution of the implicit equation system above must fulfill the equation system identically [upto the usual numerical accuracy], provided the absolute value of every flow variable in the connection set is greater than a small value (|m1.c.m_flow| > eps and |m2.c.m_flow| > eps and ... and |cM.m_flow| > eps).
[Based on the above requirements, the following implementation is recommended:
-
•
N = 1, M = 0:
inStream(.c.h_outflow) =.c.h_outflow; -
•
N = 2, M = 0:
-
•
N = 1, M = 1:
inStream(.c.h_outflow) =inStream(.h_outflow);// Additional equation to be generated.h_outflow = .c.h_outflow; -
•
N = 0, M = 2:
// Additional equation to be generatedc1.h_outflow = inStream(c2.h_outflow);c2.h_outflow = inStream(c1.h_outflow); -
•
All other cases:
if .c.m_flow.min >= 0 for all j = 1:N with j <> i and.m_flow.max <= 0 for all k = 1:MtheninStream(.c.h_outflow) = .c.h_outflow;elsesi = sum (max(-.c.m_flow,0) for j in cat(1,1:i-1, i+1:N) +sum(max( .m_flow ,0) for k in 1:M);inStream(.c.h_outflow) =(sum(positiveMax(-.c.m_flow,)*.c.h_outflow)+ sum(positiveMax(.m_flow,s_i)*inStream(.h_outflow)))/(sum(positiveMax(-.c.m_flow,s_i))+ sum(positiveMax(.m_flow,s_i)))for j in 1:N and i <> j and .c.m_flow.min < 0,for k in 1:M and .m_flow.max > 0// Additional equations to be generatedfor q in 1:M loopif .c.m_flow.min >= 0 for all j = 1:N and.m_flow.max <= 0 for all k = 1:M and k <> qthen.h_outflow = 0;else= (sum(max(-.c.m_flow,0) for j in 1:N) +sum(max( .m_flow ,0) for k in cat(1,1:q-1, q+1:M)));.h_outflow = (sum(positiveMax(-.c.m_flow,s_q)*.c.h_outflow) +sum(positiveMax(.m_flow,)* inStream(.h_outflow)))/(sum(positiveMax(-.c.m_flow,s_q)) +sum(positiveMax(.m_flow,s_q)))for j in 1:N and .c.m_flow.min < 0,for k in 1:M and k <> q and .m_flow.max > 0end for;
The operator positiveMax(-mj.c.m_flow,si) should be such that:
-
•
positiveMax(-mj.c.m_flow,si) = -mj.c_m_flow if -mj.c.m_flow>eps1j>=0, where eps1j are small flows, compared to typical problem-specific value,
-
•
all denominators should be > eps2 > 0, where eps2 is also a small flow, compared to typical problem-specific values.
Trivial implementation of positiveMax guarantees continuity of inStream():
More sophisticated implementation, with smooth approximation, applied only when all flows are small:
The derivation of this implementation is discussed in Appendix D. Note that in the cases N = 1, M =0 (unconnected port, physically corresponding to a plugged-up flange), and N = 2, M=0 (one-to-one connection), the result of inStream() is trivial and no non-linear equations are left in the model, despite the fact that the original definition equations are nonlinear.
The following properties hold for this implementation:
-
•
inStream(..) is continuous (and differentiable), provided that mj.c.h_outflow, mj.c.m_flow, ck.h_outflow, and ck.m_flow are continuous and differentiable.
-
•
A division by zero can no longer occur (since sum(positiveMax(-mj.c.m_flow,si))>=eps2 > 0), so the result is always well-defined.
-
•
The balance equations are exactly fulfilled if the denominator is not close to zero
(since the exact formula is used, if sum(positiveMax(-mj.c.m_flow,si) ) > eps). -
•
If all flows are zero, inStream(mi.c.h_outflow) = sum(mj.c.h_outflow for j<>i and mj.c.m_flow.min < 0)/Np, i.e., it is the mean value of all the Np variables mj.c.h_outflow, such that j<>i and mj.c.m_flow.min < 0. This is a meaningful approximation, considering the physical diffusion effects that are relevant at small flow rates in a small connection volume (thermal conduction for enthalpy, mass diffusion for mass fractions).
The value of relativeTolerance should be larger than the relative tolerance of the nonlinear solver used to solve the implicit algebraic equations.
As a final remark, further symbolic simplifications could be carried out by taking into account equations that affect the flows in the connection set (i.e., equivalent to mj.c.m_flow = 0, which then implies mj.c.m_flow.min >= 0). This is interesting, e.g., in the case of a valve when the stem position is set identically to closed by its controller.
]
15.3 Stream Operator actualStream
The actualStream(v) operator is provided for convenience, in order to return the actual value of the stream variable, depending on the actual flow direction. The only argument of this built-in operator needs to be a reference to a stream variable. The operator is vectorizable, in the case of vector arguments. For the following definition it is assumed that an (inside or outside) connector c contains a stream variable h_outflow which is associated with a flow variable m_flow in the same connector c:
[The actualStream(v) operator is typically used in two contexts:
In the case of equation (1), although the actualStream() operator is discontinuous, the product with the flow variable is not, because actualStream() is discontinuous when the flow is zero by construction. Therefore, a tool might infer that the expression is smooth(0, …) automatically, and decide whether or not to generate an event. If a user wants to avoid events entirely, he/she may enclose the right-hand side of (1) with the noEvent() operator.
Equations like (2) might be used for monitoring purposes (e.g. plots), in order to inspect what the ‘actual’ enthalpy of the fluid flowing through a port is. In this case, the user will probably want to see the change due to flow reversal at the exact instant, so an event should be generated. If the user doesn’t bother, then he/she should enclose the right-hand side of (2) with noEvent(). Since the output of actualStream() will be discontinuous, it should not be used by itself to model physical behaviour (e.g., to compute densities used in momentum balances) - inStream() should be used for this purpose. The operator actualStream() should be used to model physical behaviour only when multiplied by the corresponding flow variable (like in the above energy balance equation), because this removes the discontinuity.
]