Chapter 9 Connectors and Connections
This chapter covers connectors, connect-equations, and connections.
The special functions cardinality, rooted [ deprecated], Connections.isRoot, and Connections.rooted may not be used to control them.
9.1 Connect-Equations and Connectors
Connections between objects are introduced by connect-equations in the equation part of a class. A connect-equation has the following syntax:
connect ”(” component-reference ”,” component-reference ”)” ”;”
The connect-equation construct takes two references to connectors [a connector is an instance of a connector class], each of which is either of the following forms:
-
•
, where is a connector of the class, n>=1 and is a connector element of for i=1:(n-1).
-
•
m.c, where m is a non-connector element in the class and c is a connector element of m.
There may optionally be array subscripts on any of the components; the array subscripts shall be parameter expressions or the special operator “:”. If the connect construct references array of connectors, the array dimensions must match, and each corresponding pair of elements from the arrays is connected as a pair of scalar connectors.
[Example of array usage:
]
The three main tasks are to:
-
•
Elaborate expandable connectors.
-
•
Build connection sets from connect-equations.
-
•
Generate equations for the complete model.
9.1.1 Connection Sets
A connection set is a set of variables connected by means of connect-equations. A connection set shall contain either only flow variables or only non-flow variables.
9.1.2 Inside and Outside Connectors
In an element instance M, each connector element of M is called an outside connector with respect to M. All other connector elements that are hierarchically inside M, but not in one of the outside connectors of M, is called an inside connector with respect to M. This is done before resolving outer elements to corresponding inner ones.
[Example:
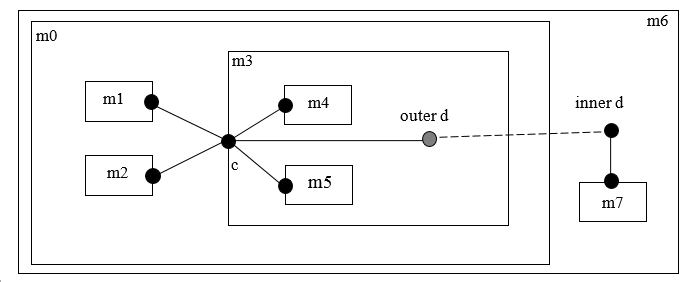
The figure visualizes the following connect equations to the connector c in the models mi. Consider the following connect equations found in the model for component m0:
and in the model for component m3 (c.x is a sub-connector inside c):
and in the model for component m6:
]
9.1.3 Expandable Connectors
If the expandable qualifier is present on a connector definition, all instances of that connector are referred to as expandable connectors. Instances of connectors that do not possess this qualifier will be referred to as non-expandable connectors.
Before generating connection equations non-parameter scalar variables and non-parameter array elements declared in expandable connectors are marked as only being potentially present. A non-parameter array element may be declared with array dimensions “:” indicating that the size is unknown. This applies to both variables of simple types, and variables of structured types.
Then connections containing expandable connectors are elaborated:
-
•
One connector in the connect equation must reference a declared component, and if the other connector is an undeclared element in a declared expandable connector it is handled as follows (elements that are only potentially present are not seen as declared):
-
–
The expandable connector instance is automatically augmented with a new component having the used name and corresponding type.
-
–
If the undeclared component is subscripted, an array variable is created, and a connection to the specific array element is performed. Introducing elements in an array gives an array with at least the specified elements, other elements are either not created or have a default value (i.e. as if they were only potentially present).
-
–
If the variable on the other side of the connect-equation is input or output the new component will be either input or output to satisfy the restrictions in section 9.3 for a non-expandable connector. [If the existing side refers to an inside connector (i.e. a connector of a component) the new variable will copy its causality, i.e. input if input and output if output, since the expandable connector must be an outside connector]. For an array the input/output property can be deduced separately for each array element.
-
–
-
•
When two expandable connectors are connected, each is augmented with the variables that are only declared in the other expandable connector (the new variables are neither input nor output). This is repeated until all connected expandable connector instances have matching variables [i.e. each of the connector instances is expanded to be the union of all connector variables.]
-
•
The variables introduced in the elaboration follow additional rules for generating connection sets (given in section 9.2).
-
•
If a variable appears as an input in one expandable connector, it should appear as a non-input in at least one other expandable connector instance in the same augmentation set. An augmentation set is defined as the set of connected expandable connector instances that through the elaboration will have matching variables.
[Example:
expandable connector EngineBusend EngineBus;block SensorRealOutput speed; // Output, i.e., non-inputend Sensor;block ActuatorRealInput speed; // Inputend Actuator;model EngineEngineBus bus;Sensor sensor;Actuator actuator;equationconnect(bus.speed, sensor.speed); // provides the non-input from sensor.speedconnect(bus.speed, actuator.speed);end Engine;]
-
•
All components in an expandable connector are seen as connector instances even if they are not declared as such [i.e. it is possible to connect to e.g. a Real variable].
[Example:
expandable connector EngineBus // has predefined signalsimport SI=Modelica.SIunits;SI.AngularVelocity speed;SI.Temperature T;end EngineBus;block SensorRealOutput speed;end Sensor;model EngineEngineBus bus;Sensor sensor;equationconnect(bus.speed, sensor.speed);// connection to non-connector speed is possible// in expandable connectorsend Engine;]
-
•
An expandable connector may not contain a component declared with the prefix flow, but may contain non-expandable connector components with flow components.
[Example:
import Interfaces=Modelica.Electrical.Analog.Interfaces;expandable connector ElectricalBusInterfaces.PositivePin p12, n12; // OKflow Modelica.SIunits.Current i; // not allowedend ElectricalBus;model BatteryInterfaces.PositivePin p42, n42;ElectricalBus bus;equationconnect(p42, bus.p42); // Adds new electrical pinconnect(n42, bus.n42); // Adds another pinend Battery;]
-
•
expandable connectors can only be connected to other expandable connectors.
If a connect equation references a potentially present variable, or variable element, in an expandable connector the variable or variable element is marked as being present, and due to the paragraphs above it is possible to deduce whether the bus variable shall be treated as input, or shall be treated as output in the connect equation. That input or output prefix is added if no input/output prefix is present on the declaration
[Example:
]
After this elaboration the expandable connectors are treated as normal connector instances, and the connections as normal connections, and all potentially present variables and array elements that are not actually present are undefined [a tool may remove them or set them to the default value, e.g. zero for Real variables]. It is an error if there are expressions referring to potentially present variables or array elements that are not actually present or non-declared variables [the expressions can only “read” variables from the bus that are actually declared and present in the connector, in order that the types of the variables can be determined in the local scope]. This elaboration implies that expandable connectors can be connected even if they do not contain the same components.
[Note that the introduction of variables, as described above, is conceptual and does not necessarily impact the flattening hierarchy in any way. Furthermore, it is important to note that these elaboration rules must consider:
-
1.
Expandable connectors nested hierarchically. This means that both outside and inside connectors must be included at every level of the hierarchy in this elaboration process.
-
2.
When processing an expandable connector that possesses the inner scope qualifier, all outer instances must also be taken into account during elaboration.
Example:
Engine system with sensors, controllers, actuator and plant that exchange information via a bus (i.e. via expandable connectors):
Due to the above connection, conceptually a connector consisting of the union of all connectors is introduced.
The engine_bus contains the following variable declarations:
]
9.2 Generation of Connection Equations
When generating connection equations, outer elements are resolved to the corresponding inner elements in the instance hierarchy (see instance hierarchy name lookup section 5.4). The arguments to each connect-equation are resolved to two connector elements.
For every use of the connect-equation
the primitive components of a and b form a connection set – together with an indication of whether they are from an inside or an outside connector; the primitive elements are of simple types – or of types defined as operator record (i.e. a component of an operator record type is not split into sub-components). The elements of the connection sets are tuples of primitive variables together with an indication of inside or outside; if the same tuple belongs to two connection sets those two sets are merged, until every tuple is only present in one set. Composite connector types are broken down into primitive components. The outer components are handled by mapping the objects to the corresponding inner components – and the inside indication is not influenced. The outer connectors are handled by mapping the objects to the corresponding inner connectors – and they are always treated as outside connectors.
[Rationale: The inside/outside as part of the connection sets ensure that connections from different hierarchical levels are treated separately. Connection sets are formed from the primitive elements and not from the connectors; this handles connections to parts of hierarchical connectors and also makes it easier to generate equations directly from the connection sets. All variables in one connection set will either be flow variables or non-flow variables due to restriction on connect-equations. The mapping from an outer to an inner element must occur before merging the sets in order to get one zero-sum equation, and ensures that the equations for the outer elements are all given for “one side” of the connector, and the inner element can define the other “side”.]
The following connection sets with just one member are also present (and merged):
-
•
Each primitive flow-variable as inside connector.
-
•
Each flow variable added during augmentation of expandable connectors, both as inside and as outside. [Note that the flow variable is not directly in the expandable connector, but in a connector inside the expandable connector.]
[Rationale: If these variables are not connected they will generate a set comprised only of this element, and thus they will be implicitly set to zero (see below). If connected, this set will be merged and adding this at the start has no impact.]
Each connection set is used to generate equations for potential and flow (zero-sum) variables of the form
-
•
a1 = a2 = ... = an; // neither flow nor stream variables
-
•
z1 + z2 + (-z3) + ... + zn = 0 ; // flow-variables
The bold-face 0 represents an array or scalar zero of appropriate dimensions (i.e. the same size as z).
For an operator record type this uses the operator ’0’ – which must be defined in the operator record; and all of the flow-variables for the operator record must be of the same operator record type. This implies that in order to have flow variables of an operator record type the operator record must define addition, negation, and ’0’; and these operations should define an additive group.
In order to generate equations for flow variables [using the flow prefix], the sign used for the connector variable zi above is +1 for inside connectors and -1 for outside connectors z3 in the example above].
[Example (simple):
The connection sets are before merging (note that one part of the load and resistor is not connected):
{<load.p.i, inside>}
{<load.n.i, inside>}
{<ground.p.i, inside>}
{<load.resistor.p.i, inside>}
{<load.resistor.n.i, inside>}
{<resistor.p.i, inside>}
{<resistor.n.i, inside>}
{<resistor.p.i, inside>, <ground.p.i, inside>}
{<resistor.p.v, inside>, <ground.p.v, inside>}
{<load.p.i, inside>, <ground.p.i, inside>}
{<load.p.v, inside>, <ground.p.v, inside>}
{<load.p.i, outside>, <load.resistor.p.i, inside>}
{<load.p.v, outside>, <load.resistor.p.v, inside>}
{<load.n.i, outside>, <load.resistor.n.i, inside>}
{<load.n.v, outside>, <load.resistor.n.v, inside>}
After merging this gives:
{<load.p.i, outside>, <load.resistor.p.i, inside>}
{<load.p.v, outside>, <load.resistor.p.v, inside>}
{<load.n.i, outside>, <load.resistor.n.i, inside>}
{<load.n.v, outside>, <load.resistor.n.v, inside>}
{<load.p.i, inside>, <ground.p.i, inside>, <resistor.p.i, inside> }
{<load.p.v, inside>, <ground.p.v, inside>, <resistor.p.v, inside>}
{<load.n.i, inside>}
{<resistor.n.i, inside>}
And thus the equations:
load.p.v = load.resistor.p.v;
load.n.v = load.resistor.n.v;
load.p.v = ground.p.v;
load.p.v = resistor.p.v;
0 = (-load.p.i) + load.resistor.p.i;
0 = (-load.n.i) + load.resistor.n.i;
0 = load.p.i + ground.p.i + resistor.p.i;
0 = load.n.i;
0 = resistor.n.i;
Example (outer component):
The connection sets are before merging (note that one part of the load and resistor is not connected):
{<load.p.i, inside>}
{<load.n.i, inside>}
{<ground.p.i, inside>}
{<resistor.p.i, inside>}
{<resistor.n.i, inside>}
{<load.p.i, inside>, <ground.p.i, inside>}
{<load.p.v, inside>, <ground.p.v, inside>}
{<load.p.i, outside>, < resistor.p.i, inside>}
{<load.p.v, outside>, <resistor.p.v, inside>}
{<load.n.i, outside>, <resistor.n.i, inside>}
{<load.n.v, outside>, <resistor.n.v, inside>}
After merging this gives:
{<load.p.i, outside>, <resistor.p.i, inside>}
{<load.p.v, outside>, <resistor.p.v, inside>}
{<load.n.i, outside>, <resistor.n.i, inside>}
{<load.n.v, outside>, <resistor.n.v, inside>}
{<load.p.i, inside>, <ground.p.i, inside>}
{<load.p.v, inside>, <ground.p.v, inside>}
{<load.n.i, inside>}
And thus the equations:
load.p.v = resistor.p.v;
load.n.v = resistor.n.v;
load.p.v = ground.p.v;
0 = (-load.p.i) + resistor.p.i;
0 = (-load.n.i) + resistor.n.i;
0 = load.p.i + ground.p.i;
0 = load.n.i;
This corresponds to a direct connection of the resistor.
]
9.3 Restrictions of Connections and Connectors
-
•
The connect-equations (and the special functions for overdetermined connectors) may only be used in equations and may not be used inside if-equations with non-parametric condition, or in when-equations. [For-equations always have parameter expressions for the array expression.]
-
•
A connector component may not be declared with the prefix parameter or constant. In the connect-equation the primitive components may only connect parameter variables to parameter variables and constant variables to constant variables.
-
•
The connect-equation construct only accepts forms of connector references as specified in section 9.1.
-
•
In a connect-equation the two connectors must have the same named component elements with the same dimensions; recursively down to the primitive components. The primitive components with the same name are matched and belong to the same connection set.
-
•
The matched primitive components of the two connectors must have the same primitive types, and flow-variables may only connect to other flow-variables, stream-variables only to other stream-variables, and causal variables (input/output) only to causal variables (input/output).
-
•
A connection set of causal variables (input/output) may at most contain variables from one inside output connector or one public outside input connector. [i.e., a connection set may at most contain one source of a signal.]
-
•
At least one of the following must hold for a connection set containing causal variables generated for a non-partial model or block:
-
1.
the connection set includes variables from an outside public expandable connector,
-
2.
the set contains variables from protected outside connectors,
-
3.
it contains variables from one inside output connector, or
-
4.
from one public outside input connector, or
-
5.
the set is comprised solely of one variable from one inside input connector that is not part of an expandable connector.
[i.e., a connection set must – unless the model or block is partial - contain one source of a signal (the last item (item 5) covers the case where a connector of a component is left unconnected and the source given textually).]
-
1.
-
•
Variables from a protected outside connector must be part of a connection set containing at least one inside connector or one declared public outside connector (i.e. it may not be an implicitly defined part of an expandable connector). [Otherwise it would not be possible to deduce the causality for the expandable connector element.]
-
•
In a connection set all variables having non-empty quantity attribute must have the same quantity attribute.
-
•
A connect equation may not (directly or indirectly) connect two connectors of outer elements. [indirectly is similar to them being part of the same connection set – however, connections to outer elements are “moved up” before forming connection sets. Otherwise the connection sets could contain “redundant” information breaking the equation count for locally balanced models and blocks.]
-
•
Subscripts in a connector reference shall be parameter expressions or the special operator “:”.
-
•
Constants or parameters in connected components yield the appropriate assert statements to check that they have the same value; connections are not generated.
-
•
For conditional connectors, see section 4.4.5.
9.3.1 Balancing Restriction and Size of Connectors
For each non-partial connector class the number of flow variables shall be equal to the number of variables that are neither parameter, constant, input, output, stream nor flow. The “number of variables” is the number of all elements in the connector class after expanding all records and arrays to a set of scalars of primitive types. The number of variables of an overdetermined type or record class (see section 9.4.1) is the size of the output argument of the corresponding equalityConstraint() function.
[Examples:
The Frame_Illegal connector (intended to be used in a simple MultiBody-package without over-determined connectors) is illegal since the number of flow and non-flow variables do not match. The solution is to create two connector classes, where two 3-vectors (e.g., a and z) are acausal Real and the other variables are matching pairs of input and output. This ensures that the models can only be connected in a tree-structure or require a “loop-breaker” joint for every closed kinematic loop:
The subsequent connectors Plug_Expanded and PlugExpanded2 are correct, but Plug_Expanded_Illegal is illegal since the number of non-flow and flow variables is different if “n” and “m” are different. It is not clear how a tool can detect in general that connectors such as Plug_Expanded_Illegal are illegal. However, it is always possible to detect this defect after actual values of parameters and constants are provided in the simulation model.
]
9.4 Equation Operators for Overconstrained Connection-Based Equation Systems
There is a special problem regarding equation systems resulting from loops in connection graphs where the connectors contain non-flow (i.e., potential) variables dependent on each other. When a loop structure occurs in such a graph, the resulting equation system will be overconstrained, i.e., have more equations than variables, since there are implicit constraints between certain non-flow variables in the connector in addition to the connection equations around the loop. At the current state-of-the-art, it is not possible to automatically eliminate the unneeded equations from the resulting equation system without additional information from the model designer.
This section describes a set of equation operators for such overconstrained connection-based equation systems, that makes it possible for the model designer to specify enough information in the model to allow a Modelica environment to automatically remove the superfluous equations.
[Connectors may contain redundant variables. For example, the orientation between two coordinate systems in 3 dimensions can be described by 3 independent variables. However, every description of orientation with 3 variables has at least one singularity in the region where the variables are defined. It is therefore not possible to declare only 3 variables in a connector. Instead n variables (n > 3) have to be used. These variables are no longer independent from each other and there are n-3 constraint equations that have to be fulfilled. A proper description of a redundant set of variables with constraint equations does no longer have a singularity. A model that has loops in the connection structure formed by components and connectors with redundant variables, may lead to a differential algebraic equation system that has more equations than unknown variables. The superfluous equations are usually consistent with the rest of the equations, i.e., a unique mathematical solution exists. Such models cannot be treated with the currently known symbolic transformation methods. To overcome this situation, operators are defined in order that a Modelica translator can remove the superfluous equations. This is performed by replacing the equality equations of non-flow variables from connection sets by a reduced number of equations in certain situations.
This section handles a certain class of overdetermined systems due to connectors that have a redundant set of variables. There are other causes of overdetermined systems, e.g., explicit zero-sum equations for flow variables, that are not handled by the method described below.]
9.4.1 Overconstrained Equation Operators for Connection Graphs
A type or record declaration may have an optional definition of function “equalityConstraint(..)” that shall have the following prototype:
The “residue” output of the equalityConstraint(..) function shall have known size, say constant n. The function shall express the equality between the two type instances T1 and T2 or the record instances R1 and R2, respectively, with a non-redundant number of equations. The residues of these equations are returned in vector “residue” of size n. The set of n non-redundant equations stating that R1 = R2 is given by the equation (0 characterizes a vector of zeros of appropriate size):
[If the elements of a record Record are not independent from each other, the equation “R1 = R2” contains redundant equations].
A type class with an equalityConstraint function declaration is called overdetermined type. A record class with an equalityConstraint function definition is called overdetermined record. A connector that contains instances of overdetermined type and/or record classes is called overdetermined connector. An overdetermined type or record may neither have flow components nor may be used as a type of flow components. If an array is used as argument to any of the Connections.* functions it is treated as one unit – there is no special treatment of this case – however, there is for connect – see section 9.1.
Every instance of an overdetermined type or record in an overdetermined connector is a node in a virtual connection graph that is used to determine when the standard equation “R1 = R2” or when the equation “0 = equalityConstraint(R1,R2)”has to be used for the generation of connect(...) equations. The branches of the virtual connection graph are implicitly defined by “connect(..)” and explicitly by Connections.branch(...) statements, see table below. Connections is a built-in package in global scope containing built-in operators. Additionally, corresponding nodes of the virtual connection graph have to be defined as roots or as potential roots with functions Connections.root(...) and Connections.potentialRoot(...), respectively. In the following table, A and B are connector instances that may be hierarchically structured, e.g., A may be an abbreviation for EnginePort.Frame.
| connect(A,B); | Defines breakable branches from the overdetermined type or record instances in connector instance A to the corresponding overdetermined type or record instances in connector instance B for a virtual connection graph. The types of the corresponding overdetermined type or record instances shall be the same. | |||
| Connections.branch(A.R,B.R); | Defines a non-breakable branch from the overdetermined type or record instance R in connector instance A to the corresponding overdetermined type or record instance R in connector instance B for a virtual connection graph. This function can be used at all places where a connect(..) statement is allowed [e.g., it is not allowed to use this function in a when-clause. This definition shall be used if in a model with connectors A and B the overdetermined records A.R and B.R are algebraically coupled in the model, e.g., due to B.R = f(A.R, <other unknowns>)]. | |||
| Connections.root(A.R); | The overdetermined type or record instance R in connector instance A is a (definite) root node in a virtual connection graph. [This definition shall be used if in a model with connector A the overdetermined record A.R is (consistently) assigned, e.g., from a parameter expressions] | |||
|
The overdetermined type or record instance R in connector instance A is a potential root node in a virtual connection graph with priority “p” (). If no second argument is provided, the priority is zero. “p” shall be a parameter expression of type Integer. In a virtual connection subgraph without a Connections.root definition, one of the potential roots with the lowest priority number is selected as root [This definition may be used if in a model with connector A the overdetermined record A.R appears differentiated – der(A.R) – together with the constraint equations of A.R, i.e., a non-redundant subset of A.R maybe used as states] | |||
| b = Connections.isRoot(A.R); | Returns true, if the overdetermined type or record instance R in connector instance A is selected as a root in the virtual connection graph. | |||
|
If the operator Connections.rooted(A.R) is used, or the equivalent but deprecated operator rooted(A.R), then there must be exactly one statement Connections.branch(A.R,B.R) involving A.R (the argument of Connections.rooted must be the first argument of Connections.branch). In that case Connections.rooted(A.R) returns true, if A.R is closer to the root of the spanning tree than B.R; otherwise false is returned. [This operator can be used to avoid equation systems by providing analytic inverses, see Modelica.Mechanics.MultiBody.Parts.FixedRotation.] |
[Note, that Connections.branch, Connections.root, Connections.potentialRoot do not generate equations. They only generate nodes and branches in the virtual graph for analysis purposes.]
9.4.2 Converting the Connection Graph into Trees and Generating Connection Equations
Before connect(...) equations are generated, the virtual connection graph is transformed into a set of spanning trees by removing breakable branches from the graph. This is performed in the following way:
-
1.
Every root node defined via the “Connections.root(..)” statement is a definite root of one spanning tree.
-
2.
The virtual connection graph may consist of sets of subgraphs that are not connected together. Every subgraph in this set shall have at least one root node or one potential root node in a simulation model. If a graph of this set does not contain any root node, then one potential root node in this subgraph that has the lowest priority number is selected to be the root of that subgraph. The selection can be inquired in a class with function Connections.isRoot(..), see table above.
-
3.
If there are n selected roots in a subgraph, then breakable branches have to be removed such that the result shall be a set of n spanning trees with the selected root nodes as roots.
After this analysis, the connection equations are generated in the following way:
-
1.
For every breakable branch [i.e., a connect(A,B) equation,] in one of the spanning trees, the connection equations are generated according to section 9.2.
-
2.
For every breakable branch not in any of the spanning trees, the connection equations are generated according to section 9.2, except for overdetermined type or record instances R. Here the equations “0 = R.equalityConstraint(A.R,B.R)” are generated instead of “A.R = B.R”.
9.4.3 Examples of Overconstrained Connection Graphs
[Example:
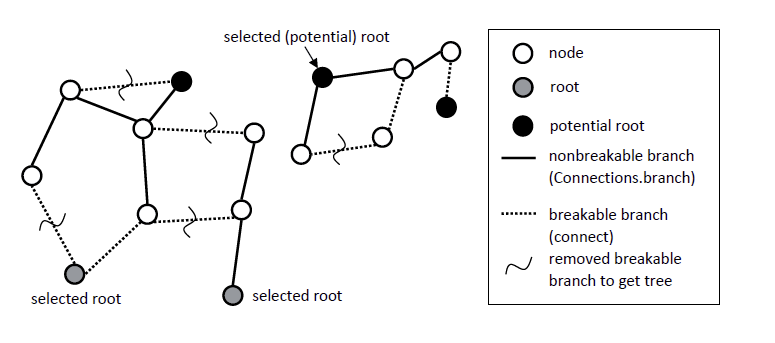
]
9.4.3.1 An Overdetermined Connector for Power Systems
[An overdetermined connector for power systems based on the transformation theory of Park may be defined as:
The currents and voltages in the connector are defined relatively to the harmonic, high-frequency signal of a power source that is essentially described by angle theta of the rotor of the source. This allows much faster simulations, since the basic high frequency signal of the power source is not part of the differential equations. For example, when the source and the rest of the line operates with constant frequency (= nominal case), then AC_Plug.v and AC_Plug.i are constant. In this case a variable step integrator can select large time steps. An element, such as a 3-phase inductor, may be implemented as:
At the place where the source frequency, i.e., essentially variable theta, is defined, a Connections.root(..) must be present:
The graph analysis performed with the virtual connection graph identifies the connectors, where the AC_Angle needs not to be passed between components, in order to avoid redundant equations.
9.4.3.2 An Overdetermined Connector for 3-dimensional Mechanical Systems
An overdetermined connector for 3-dimensional mechanical systems may be defined as:
A fixed translation from a frame A to a frame B may be defined as:
Since the transformation matrix frame_a.R is algebraically coupled with frame_b.R, a branch in the virtual connection graph has to be defined. At the inertial system, the orientation is consistently initialized and therefore the orientation in the inertial system connector has to be defined as root:
]